三角形 の 外角 の 定理 470638-直角三角形 角度 求め方 斜辺 高さ
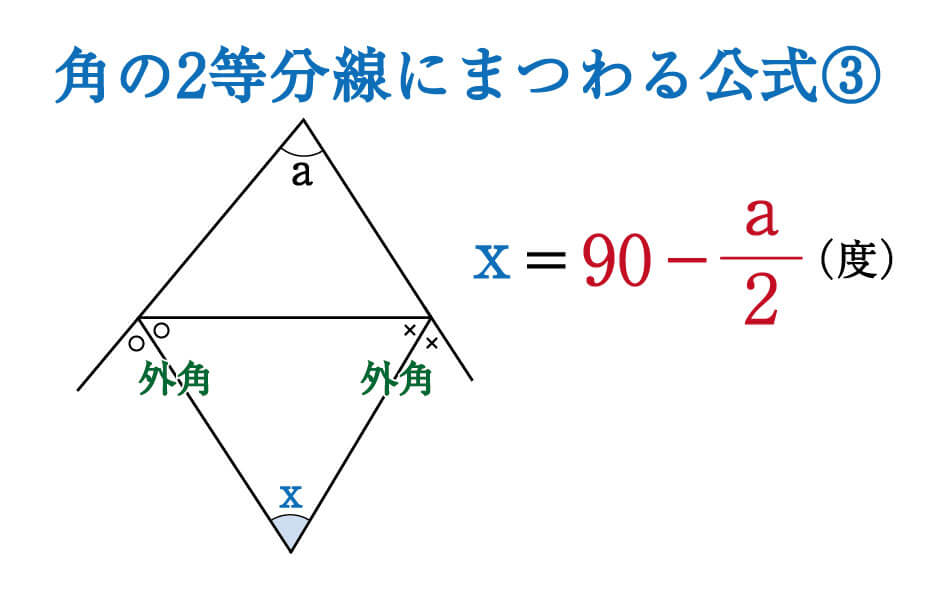
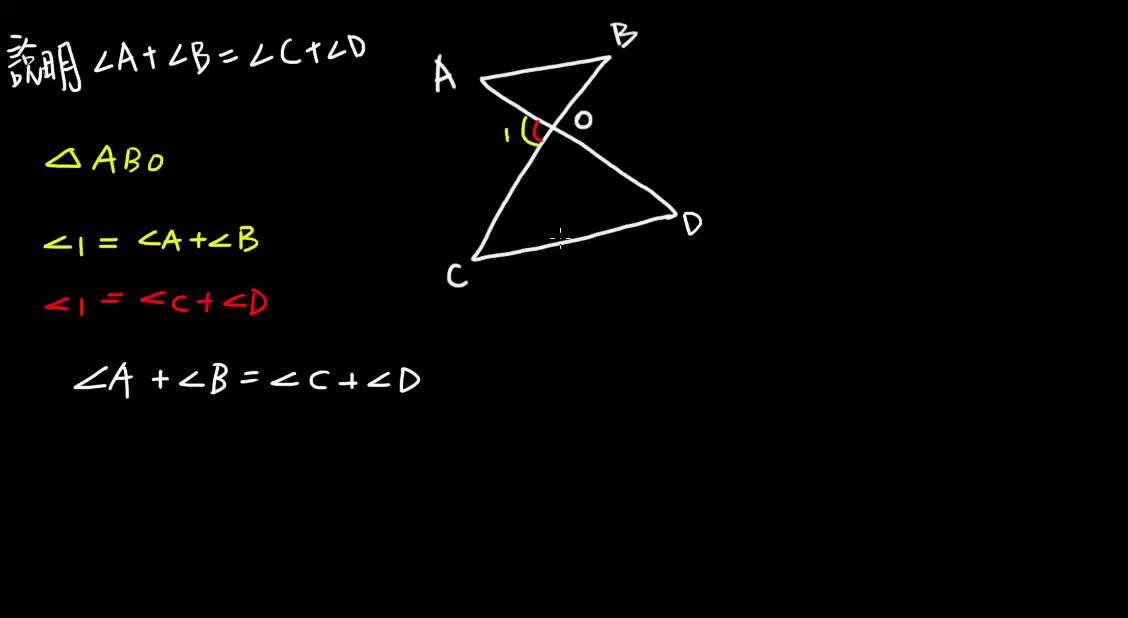
角B=180°-(30°+45°) =180°-75° =105° と計算できます。 この角Aように、あらかじめわかる角度を図に記入して、三角形の内角と外角の関係(三角の旗)を利用すると簡単に正解が得られる問題はたくさんあります。 答え 角A=1°、角B=105° 三角形の角の2等分線と比例 三角形の内角、外角の二等分線での内分点、外分点の関係性 で およびその外角の二等分線が直線AB上に交わる点をM、Nとすると となり、逆も成り立つ。 また上の式が成り立つとき、 、 は を調和に分けるといいブーメラン型の図形を見ていきます。 すると、赤い三角形の外角を と表すことができます。 次に右下にある三角形に注目して 同じように外角を考えると 外角の大きさは と表すことができます。 よって、凹みの部分の角が となるので とがっている角
3分でわかる 三角形の外角の定理の証明 Qikeru 学びを楽しくわかりやすく
直角三角形 角度 求め方 斜辺 高さ
直角三角形 角度 求め方 斜辺 高さ-底角 ⇒ 二等辺三角形の底辺の両端の角 頂角 ⇒ 二等辺三角形の頂部の角 頂角の詳細は下記をご覧ください。 頂角とは?1分でわかる意味、読み方、求め方、二等辺三角形との関係、底角との違い まとめ 今回は底角について説明しました。 角と三角形の分類 定義 鋭角 : 0∘ 0 ∘ より大きく 90∘ 90 ∘ より小さい角 鈍角 : 90∘ 90 ∘ より大きく 180∘ 180 ∘ より小さい角 鈍角三角形 :3つの内角が鋭角である三角形 直角三角形 :1つの内角が直角である三角形 鈍角三角形 :1つの内角が




角の二等分線の定理 内分点 外分点での辺の比と証明問題 Hatsudy 総合学習サイト
この定理の証明過程により,1辺と他の2辺の延長線に接する円が存在する. この円を 傍接円 といい,傍接円の中心を 傍心 という.1つの三角形に対して,傍接円,傍心が3個ずつ存在する. 図の点 I I は, ABCの内心であり,また対頂角が等しいことなどに外角=外角と隣り合わない内角の和 例えば下図の三角形の外角=3050=80度です。 上式を覚えておけば簡単に外角が算定できます。 なぜ外角=外角と隣り合わない内角の和となるか解説します。 三角形の内角の和は180度です。 角度の大きさをA、B、Cと 垂心 :三角形の3つの頂点から向かい合う辺に下ろした垂線の交点 傍接円 :三角形の1辺と他の2辺の延長に接する円 傍心 :傍接円の中心 ※傍心・傍接円は3つある。 定理 外心 三角形の3辺の垂直二等分線は1点で交わる。 内心 三角形の3つの内角
二等分線の性質の逆 角の二等分線の長さ 三角形の内角・外角の二等分線の性質は,中学数学で習う基本的で重要な性質です.それらの主張とその証明を紹介します.さらに,後半では発展的内容として,角の二等分線の長さについても紹介します. ⇨ 三角形の相似による証明 証明 Cを通りAQに平行な線とABの交点をEとし、BAの先をOとする。 AQとECは平行であるため錯角と同位角より ∠AEC=∠ACE=∠CAQ=∠OAQ よって AECは二等辺三角形である。 なので AE=AC ① また EBC∽ ABQなので三角形の内角と外角の性質は次の $2$ つとなります。 ① 三角形の内角の和は $\textcolor{blue}{180°}$ である ② 三角形の外角は、それととなり合わない $\textcolor{blue}{2}$ つの内角の和に等しい まずは、① 三角形の内角の和は $180°$ である について、なぜそうなるのか確認
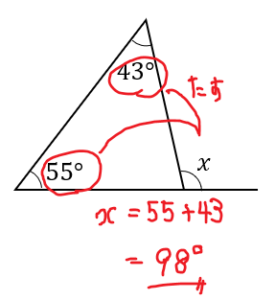
中2数学 図形 三角形の内角と外角の関係 ① 「三角形の外角はそれととなり合わない2つの内角の和に等しい」 より x = 70°42° = 112° ② x 41° 17° A D 50° 23° B C E 73° BCEにおいて 三角形の外角はそれととなり合わない2つの内角の和に等しいので ∠ABE = 50外角 解説 ∠Cの 外角 とは右図のような角をいいます. ∠Cの外角はBCを延長してAC側にできるものと,ACを延長してBC側にできるものの2つあります.これら2つの外角はいずれも 180゚-∠C です. <性質> 三角形の1つの角の外角は残り2つの内角の和外角の和とは? 言葉の意味 多角形 多角形とは、3つ以上の線分で囲まれた図形のことを言います。 これだけ聞くと、イメージしにくいかもしれませんが、私たちがよく目にする三角形や四角形、六角形も多角形に当てはまります。 多角形の中には、正多角形というものもあります。




数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



3分なるほど 三角形の内角 外角の性質について解説 数スタ
22/7/19 3 0 回答 三角形の外心 垂心 類似重心 (ルモアーヌ点)は双曲線上にあるという定理があるようですが、その証明は調べた限りでは見つけることはできませんでした。 どなたか証明していただける方おられましたらよろしくお願い致します。 数学 ・ 外角定理 外角定理の概要 ナビゲーションに移動検索に移動証明 外角定理を表した図。 abcにおいて、辺 bc を頂点 c 側に延長した線上に点 p をとる(∠bca の外角が ∠acp となる)。ここで、三角形の内角の和は 1三角形の内角三角形の内角の和は \(180°\) である。内角とは、内側の角のことですね。三角形の \(3\) つの内角の大きさをすべて、足すと \(180°\) 、つまり一直線になるということです。三角形がどんな形であっても成り立ちます。




三角形の内角の和は180度って証明できるの 三角形の外角の定理 公式 や問題アリ 遊ぶ数学



数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
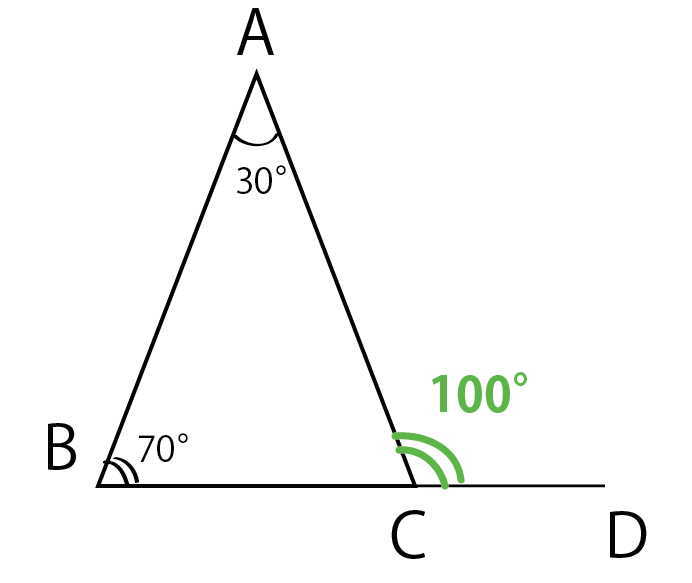
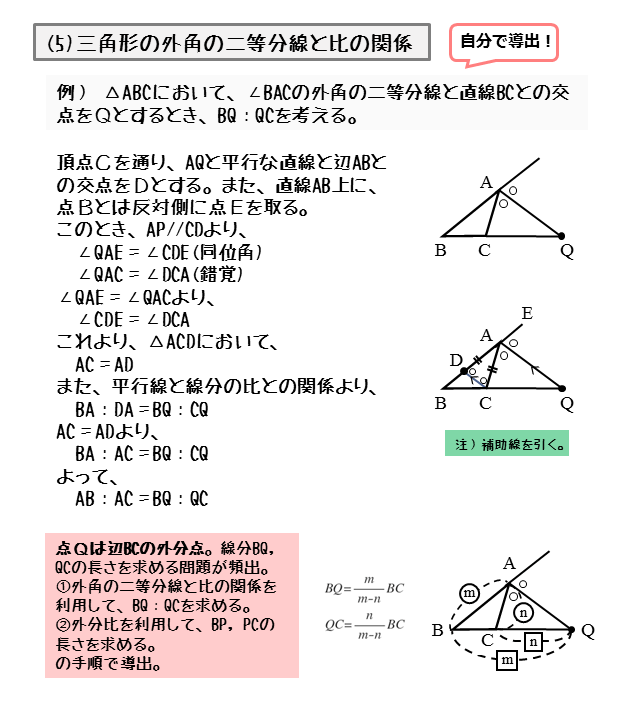
三角形の外角 赤色の角度のことを、ぜんぶ 「外角」 と呼ぶよ! 三角形の1辺を延長して外角を理解しよう! 三角形の1つの外角は、その隣にない2つの内角の和と等しい はい。これ意味わかる・・・?クソわかりづらいよね?ウンウン。。 下の図で解説※ 三角形の内角の和は180度 ※ 三角定規は30度・60度と,45度・45度 ※ 複雑な図形の問題では,二等辺三角形をさがす ※ 外角の定理を利用できるようにする 目 次 基本1 p2 基本2 p4 基本3 p5 基本4 p6 練習1 p7 練習2 p8 練習3 p9 練習4 p11MathAquarium定理・公式の証明三角形の角の二等分線と比 2 2 AB>AC である ABC の∠A の外角の二等分線と 直線BC の交点をQ とする。すなわち, ∠XAQ=∠CAQ のとき,次の等式が成り立つ。 AB:AC=BQ:CQ 証明 点C を通り直線AQ と平行な直線と,辺AB との
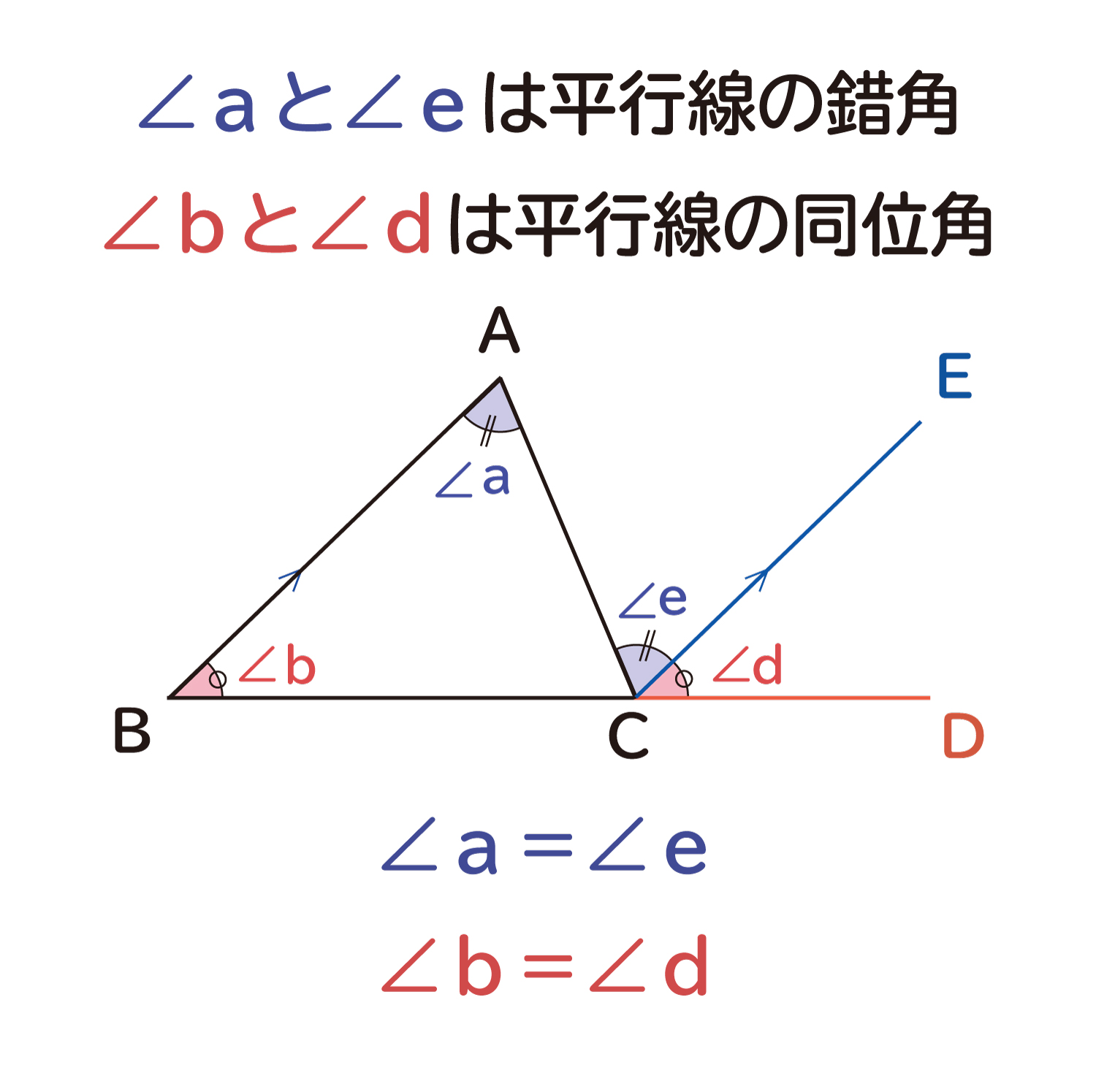



なぜ 三角形の1つの外角は それと隣り合わない2つの内角の和に等しい のか を説明します おかわりドリル




外角 の 定理 3分なるほど 三角形の内角 外角の性質について解説 Stg Origin Aegpresents Com
以上、ピタゴラスの定理の逆の証明を紹介してきました。 「直角三角形ならば a^2b^2=c^2 a2 b2 = c2 」だけでなく、その等式が成り立つならば直角三角形である、という角度を決めるような等式ですね。 これはピタゴラスの定理の一般化、(第二)余弦定理 先生 (1)三角形の内角の和と外角の定理を利用して、三角形の角の大きさを求めましょう。 まず、内角と外角とは何か学んでいきましょう。 三角形の内角の和は、全ての 多角形 たかっけい の角度を求めるときの基礎です。 三角形の内角の和というの こんにちは、ウチダです。 今日は、中学2年生で詳しく学ぶ 「三角形の内角の和」 について、それが180度である証明や、三角形の外角に関する公式・問題を解説していきます。 また、記事の後半では「内角の和が270度である三角形」についても考察し



3




角度の計算 裏技まとめ 教遊者
正弦定理を使った場合の解の絞り込みに使えるのが、今回の「 三角形の辺と角の関係 」です。 角の大きさが大きい ほど、それに対する辺の大きさも大きくなる ことから、 $~\sin{A}=\displaystyle \frac{\sqrt{3}}{2}~$を満たす$~A~$を、次のように問題を解き切ることがこの問題を解くためには、①二等辺三角形の性質、②三角形の外角の定理、を理解しておく必要があります。 二等辺三角形の性質は以下の通りです。 1.2辺の長さが等しい 2 2つの底角が等しい 3 頂角の2等分線は底辺を垂直に2等分する三角形(さんかくけい、さんかっけい、拉 triangulum, 独 Dreieck, 英, 仏 triangle, (古風) trigon)は、同一直線上にない3点と、それらを結ぶ3つの線分からなる多角形。 その3点を三角形の頂点、3つの線分を三角形の辺という。 記法・定義 点A, 点B, 点C を頂点とする三角形は記号 を用いて ABC と表
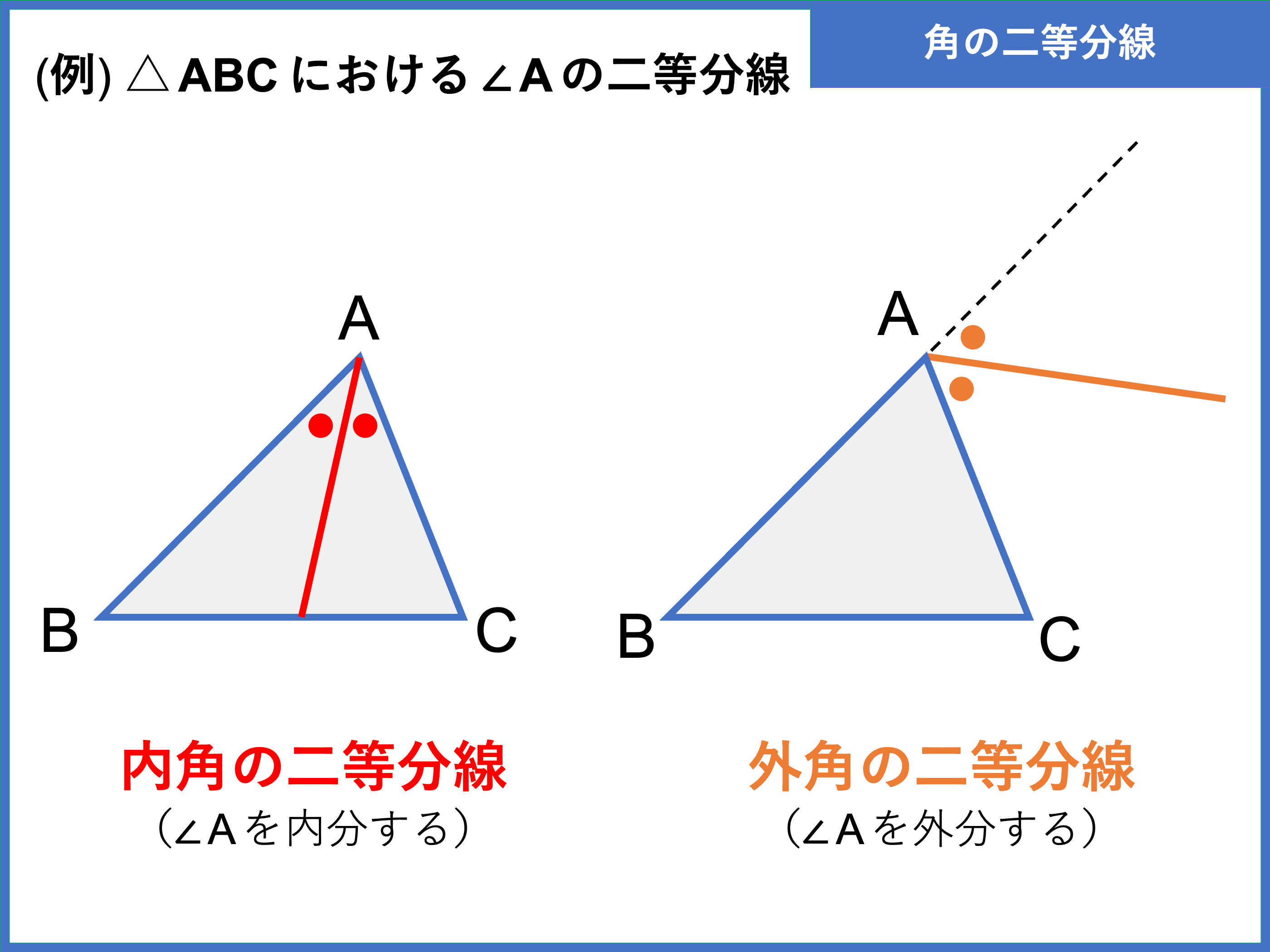



角の二等分線とは 外角 内角の定理や性質をわかりやすく解説 受験辞典



角の二等分線とは 外角 内角の定理や性質をわかりやすく解説 受験辞典
2直線が交わって角を作るとき,となり同士の角の大きさが等しいならば, 等しい大きさ それぞれ「直角」 それぞれの角を直角であるという. ~次を認める~ ① 2つの三角形において,2辺とその間の角がそれぞれ等しいならば,




陳易數學 三角形的外角和 三角形的外角定理 陳易數學 懶人公式包 公式懶人包 Facebook



三角形の外角定理について教えてちょんまげ これでどうですか Yahoo 知恵袋




角の二等分線が図で誰でも一発でわかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ
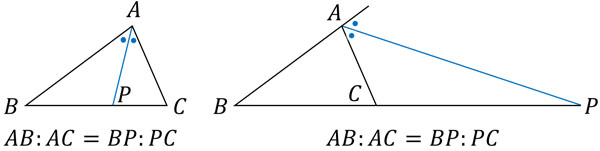



角の二等分線の定理 内分点 外分点での辺の比と証明問題 Hatsudy 総合学習サイト
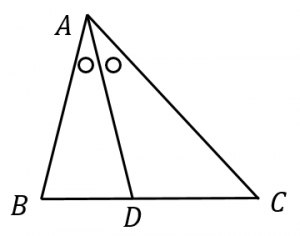



角の二等分線定理 内角 外角それぞれ 具体例で学ぶ数学
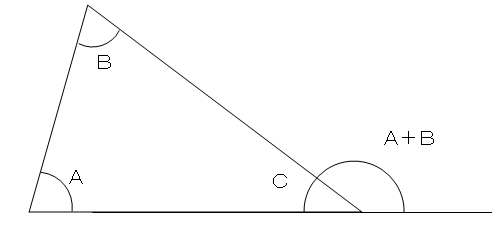



三角形の内角と外角の関係




角の2等分線の定理 幾何 数学a フリー教材開発コミュニティ Ftext



多角形とは 外角 内角の和 面積 対角線の公式と求め方 受験辞典




陳易數學 三角形的外角和 三角形的外角定理 陳易數學 懶人公式包 公式懶人包 Facebook




3分でわかる 三角形の外角の定理の証明 Qikeru 学びを楽しくわかりやすく




ブーメラン型四角形 凹四角形 の角度を求める方法 Qikeru 学びを楽しくわかりやすく
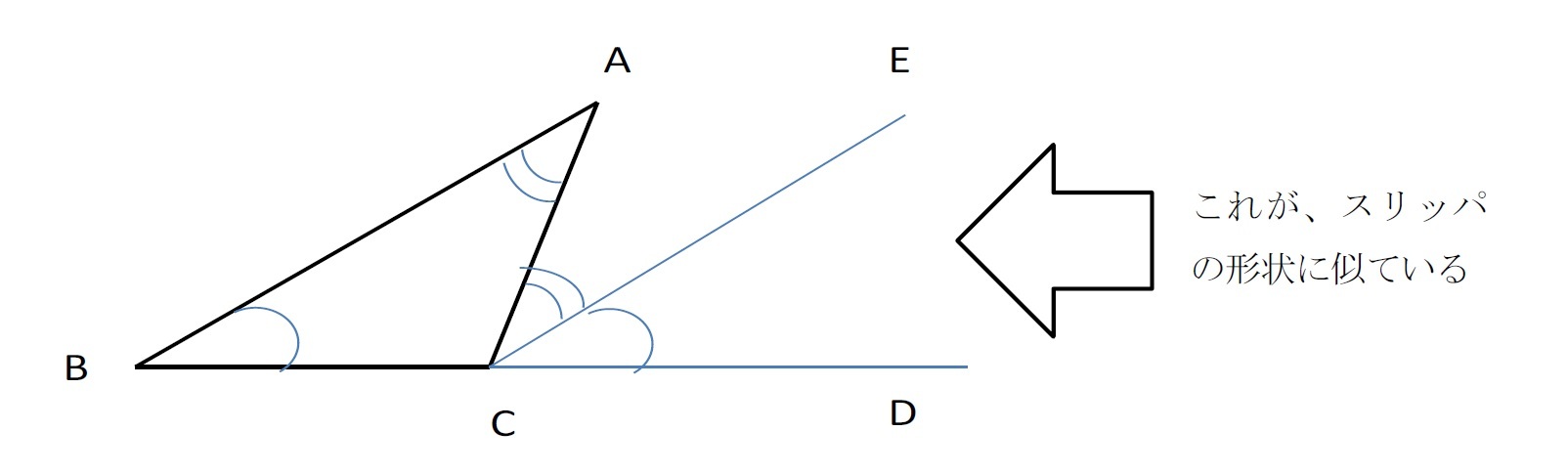



スリッパの法則 って 知っていますか ニッセイ基礎研究所



三角形の角の二等分線定理 外角




算数の問題でもあり 数学の問題でもありますの解答解説2 に代えて Fitのひろば




中2数学 複雑な多角形 角の和 応用問題



私立中学入試対策 角度の問題 二等辺三角形 外角の定理 個人契約 福岡 家庭教師 ふなきち




三角形の外角の2等分線 Schoolmath S Diary
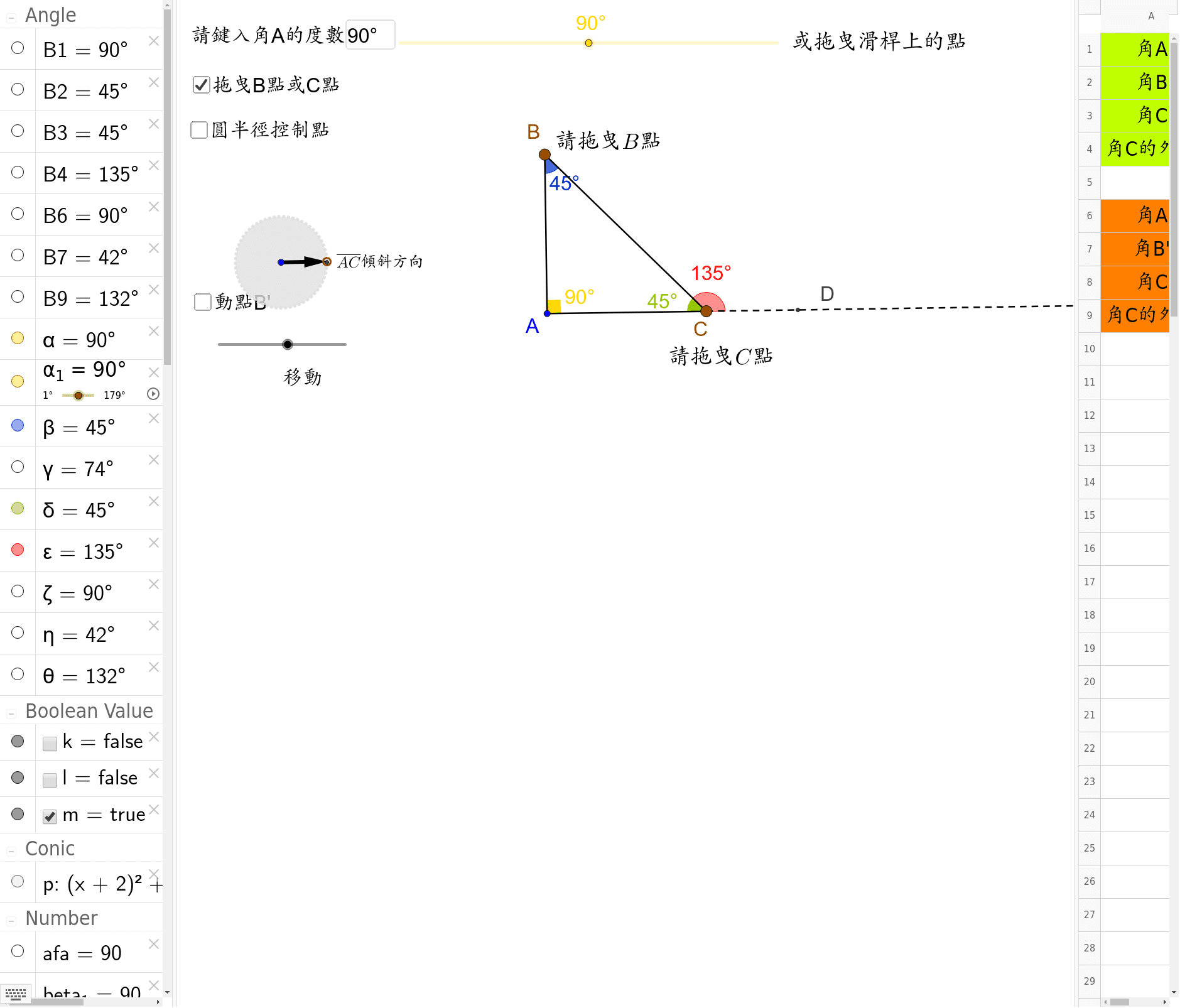



探索三角形外角定理 Geogebra



1
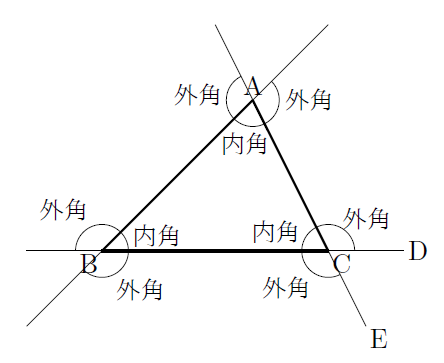



三角形の内角と外角 まなびの学園
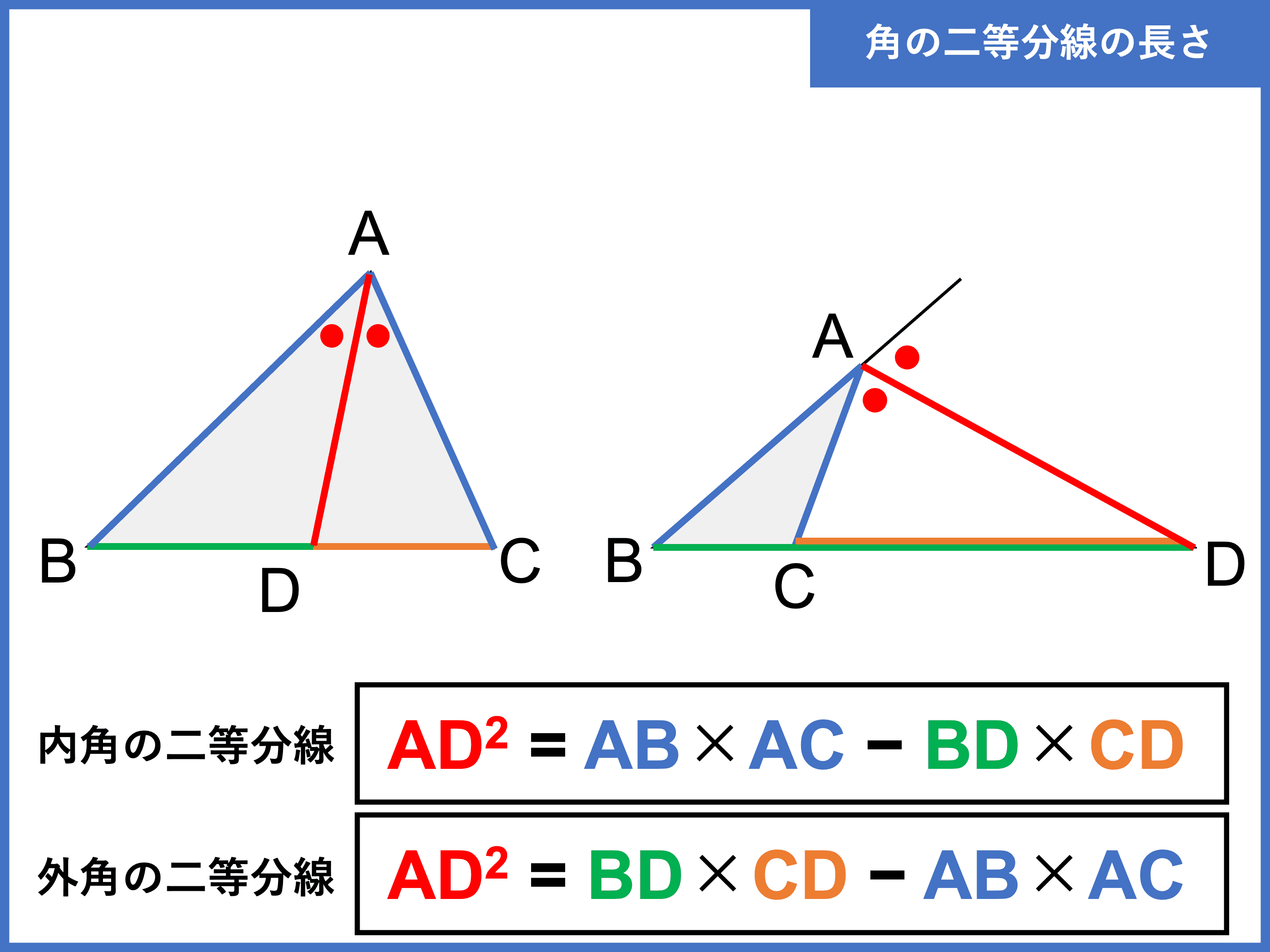



角の二等分線とは 外角 内角の定理や性質をわかりやすく解説 受験辞典



2
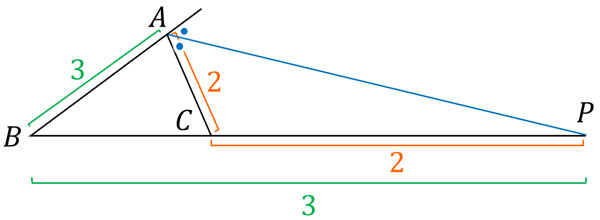



角の二等分線の定理 内分点 外分点での辺の比と証明問題 Hatsudy 総合学習サイト
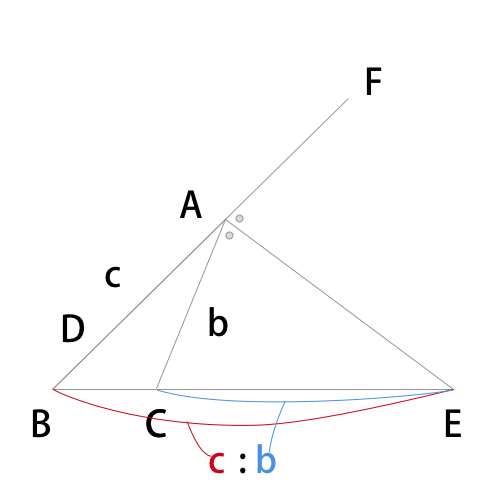



外角の2等分線の定理とその証明



1
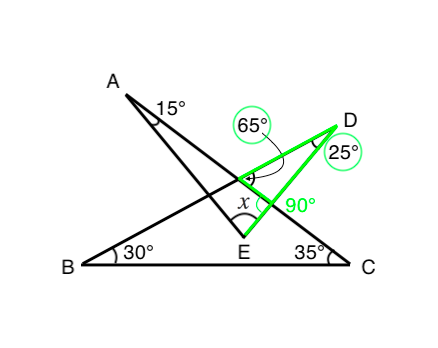



角度を求める問題 スリッパを探そう 苦手な数学を簡単に




外角定理外角定理 Kmbymh




三角形外角定理之推導 Live 多媒體數學觀念典online




高校数学a 外角の二等分線と比 練習編 映像授業のtry It トライイット
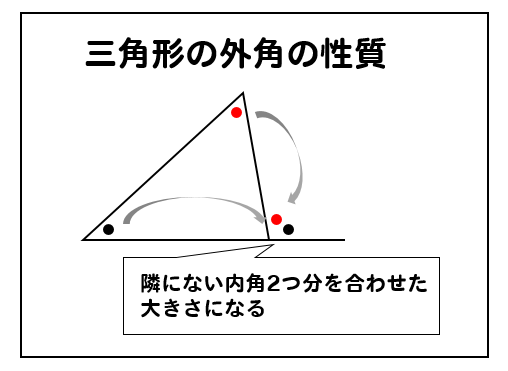



中2数学 ブーメラン型角度の求め方を解説 数スタ



3



外角 の 定理 3分なるほど 三角形の内角 外角の性質について解説 Stg Origin Aegpresents Com



今井塾セミナー



呷意小棧 三角形的外角定理
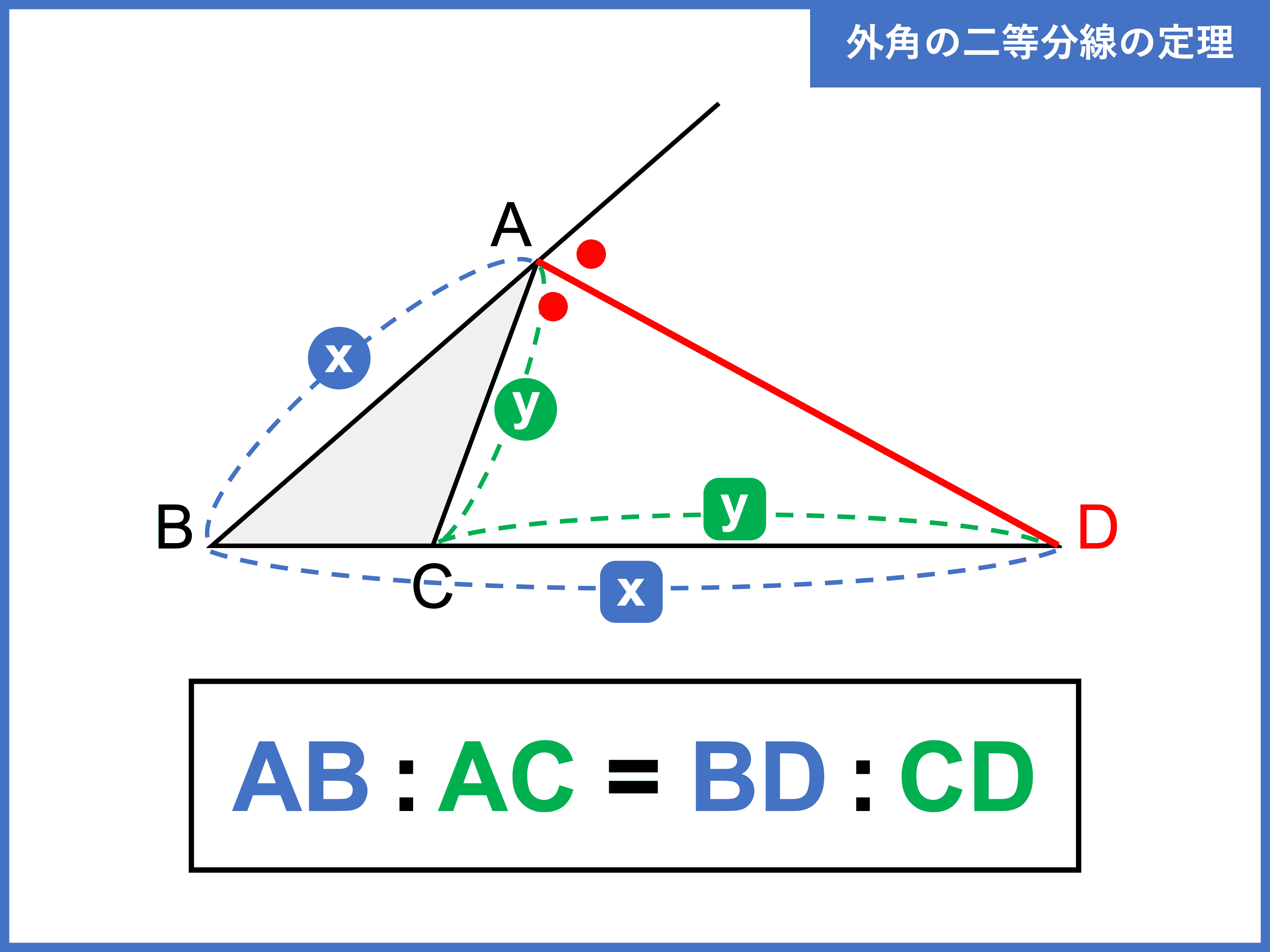



角の二等分線とは 外角 内角の定理や性質をわかりやすく解説 受験辞典




内角の和 180 N 2 外角の和 360 教遊者
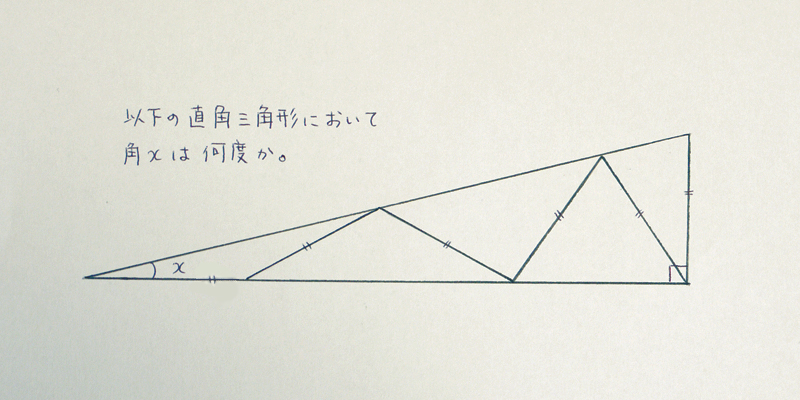



ナー 娘が外角定理を習ったので 有名な美しい問題を出してみたら んーーー 見た感じ15度に見える と まさかのアプローチで正答を出されて参りました T Co J1evbvva6y Twitter




中3数学 円周角 三角形の外角の関係を使う問題 Youtube



傍接円 傍心について
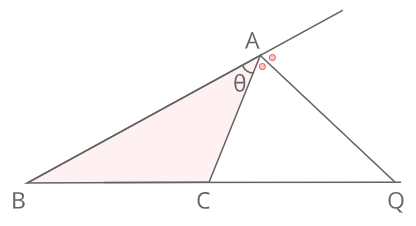



高校数学 外角の二等分線と比 の公式とその証明 Enggy




外角の求め方 外角の和を使って多角形の角度を求める問題 中学や高校の数学の計算問題




中2数学 複雑な多角形 角の和 応用問題




3分でわかる 三角形の外角の定理の証明 Qikeru 学びを楽しくわかりやすく




外角 の 定理 3分なるほど 三角形の内角 外角の性質について解説 Stg Origin Aegpresents Com
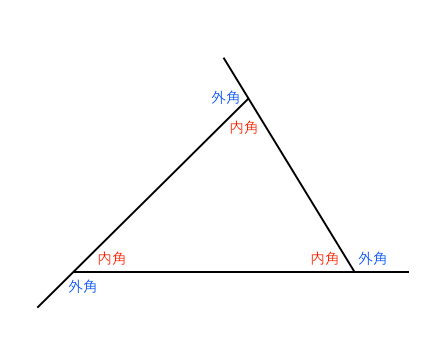



図形の調べ方 外角を求める 苦手な数学を簡単に




外角の定理 数学について考えてみる




角の二等分線の定理 内分点 外分点での辺の比と証明問題 Hatsudy 総合学習サイト




三角形の角度を求める問題 小学生 中学生の勉強




外角 の 定理 3分なるほど 三角形の内角 外角の性質について解説 Stg Origin Aegpresents Com
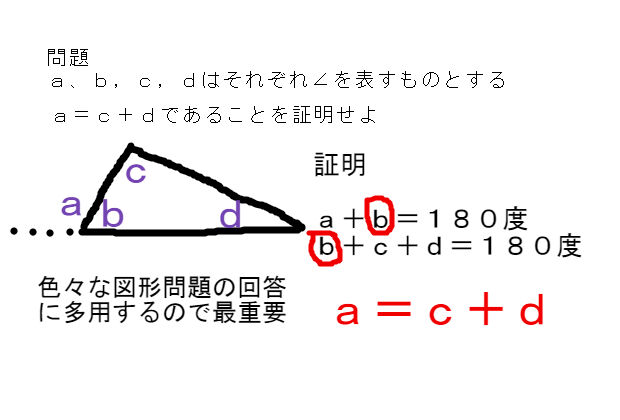



一番覚えやすい三角形の外角定理 中学 数学 理科の復習サイト




中2数学 三角形の内角と外角 例題編 映像授業のtry It トライイット




角の二等分線定理 感じる科学 味わう数学



角の二等分線とは 外角 内角の定理や性質をわかりやすく解説 受験辞典
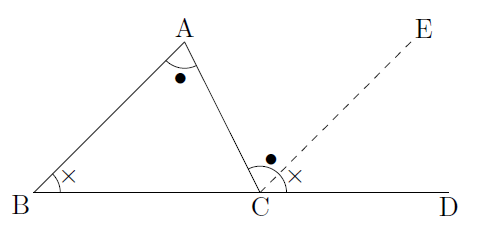



三角形の内角と外角 まなびの学園




角の2等分線の定理 数学i フリー教材開発コミュニティ Ftext




数a 外角二等分線の定理が簡単に覚えられる かつ忘れない方法 個太郎塾ふじみ野教室




3分でわかる 三角形の外角の定理の証明 Qikeru 学びを楽しくわかりやすく




内角と外角の違いがチェバとメネラウスの違いに行き着く件 感じる科学 味わう数学
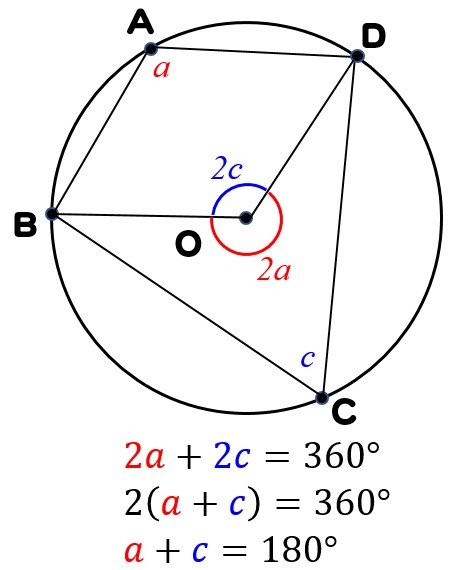



円周角の定理の解説 問題の解き方 数学fun



数学中2三角形の角度を求める問題です 角abcがどうして2a Yahoo 知恵袋
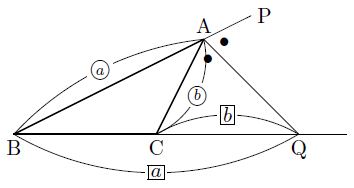



外角の2等分線と線分の比 まなびの学園



三角形內角定理與外角定理應用 三角形與多邊形的角度 均一教育平台



私立中学入試対策 角度の問題 二等辺三角形 外角の定理 個人契約 福岡 家庭教師 ふなきち
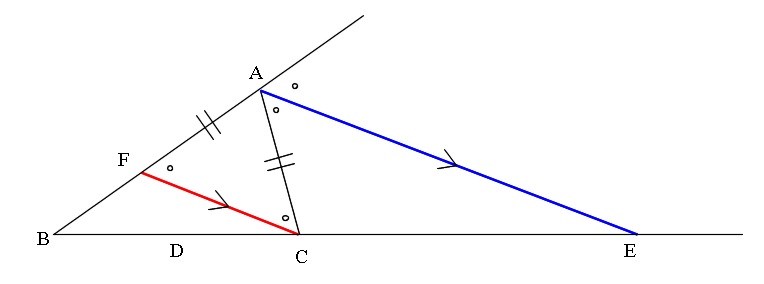



内角の二等分線と外角の二等分線の定理の覚え方と使い方



凹んだ四角形の内角と外角の関係 中2 tさんからの質問に答えますv O A Day In Our Life




高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月



角の二等分線の定理 内分点 外分点での辺の比と証明問題 Hatsudy 総合学習サイト



図形の性質 角の二等分線と比について 日々是鍛錬 ひびこれたんれん
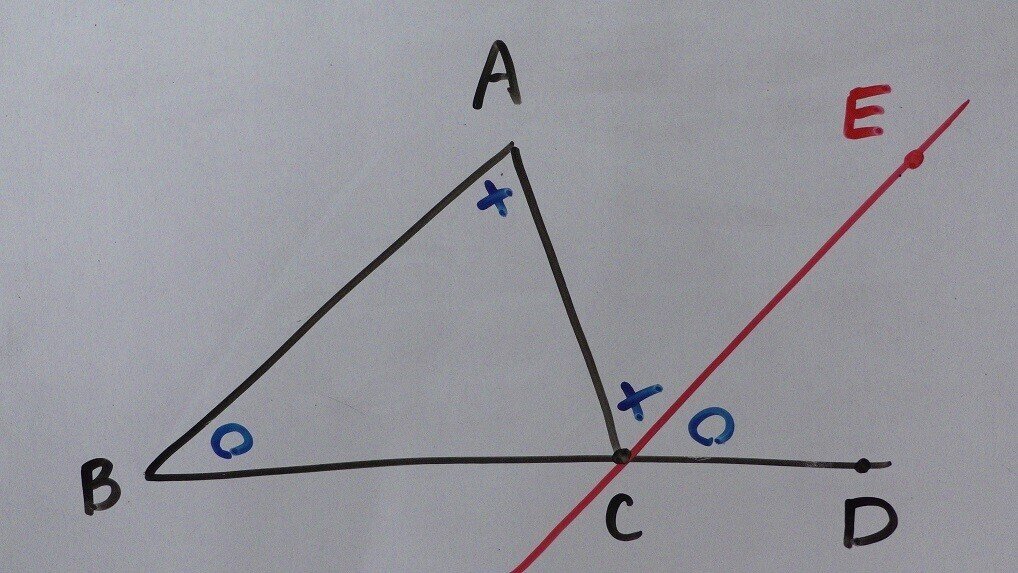



11 6 平行線の幾何 内対角定理 理一の数学事始め Note



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学
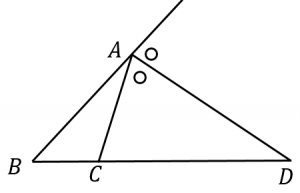



角の二等分線定理 内角 外角それぞれ 具体例で学ぶ数学
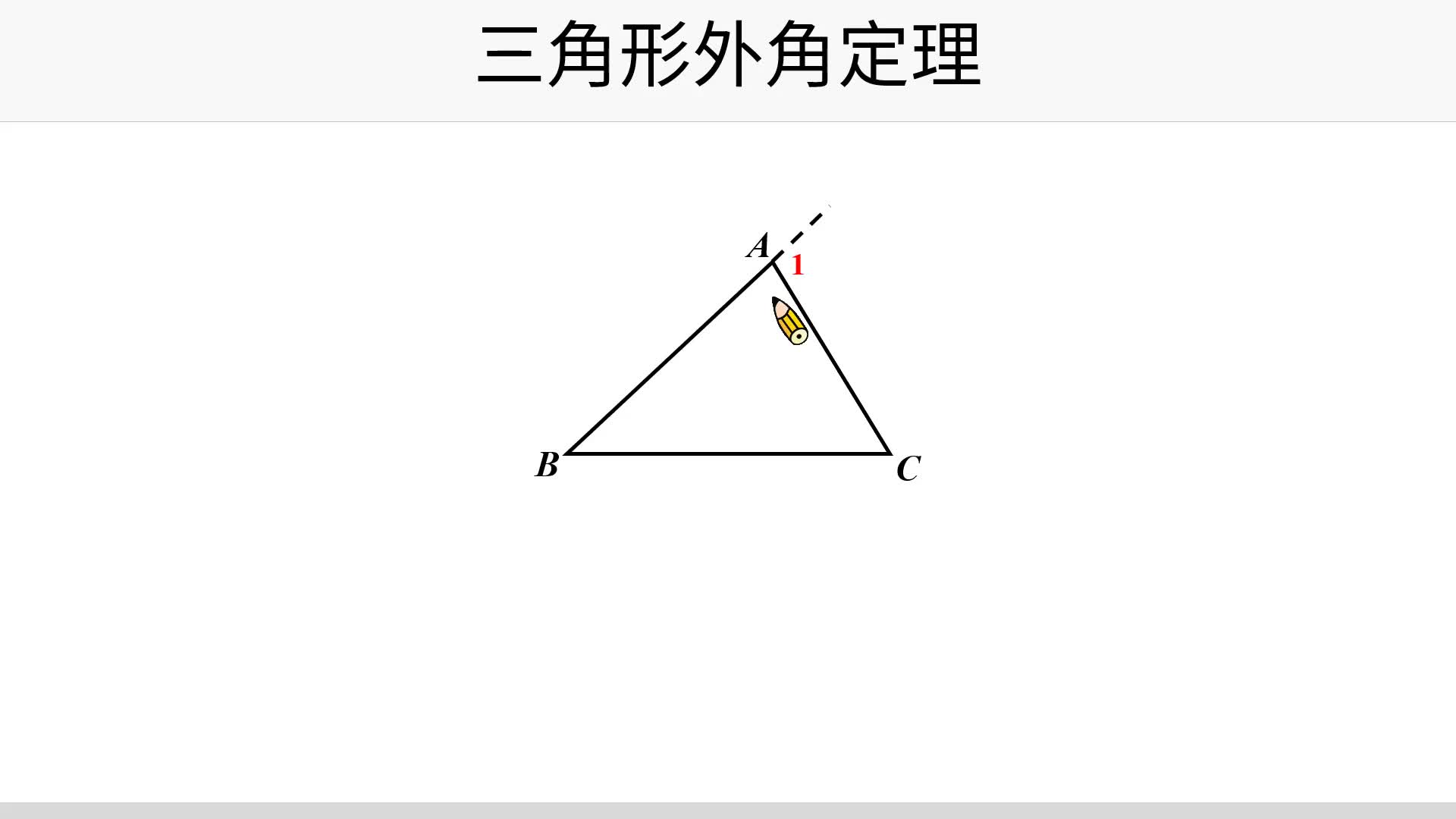



三角形外角定理 台灣數位學苑 K12 數學




数学 中2 48 三角形の内角と外角 基本編 Youtube




第1巻命題16 三角形の外角は内対角より大きい Stoixeia ストイケイア




三角形外角定理 Youtube




内角の二等分線 外角の二等分線の比の定理 証明 Youtube




高校数学b 角の二等分線のベクトル2パターン 受験の月




三角形の内角の和は180度って証明できるの 三角形の外角の定理 公式 や問題アリ 遊ぶ数学




角の2等分線によって分ける比 身勝手な主張




サクッと解説 角の二等分線と比の特徴となぜ について 数スタ




外角の難問 市ヶ谷 中学受験credoのブログ
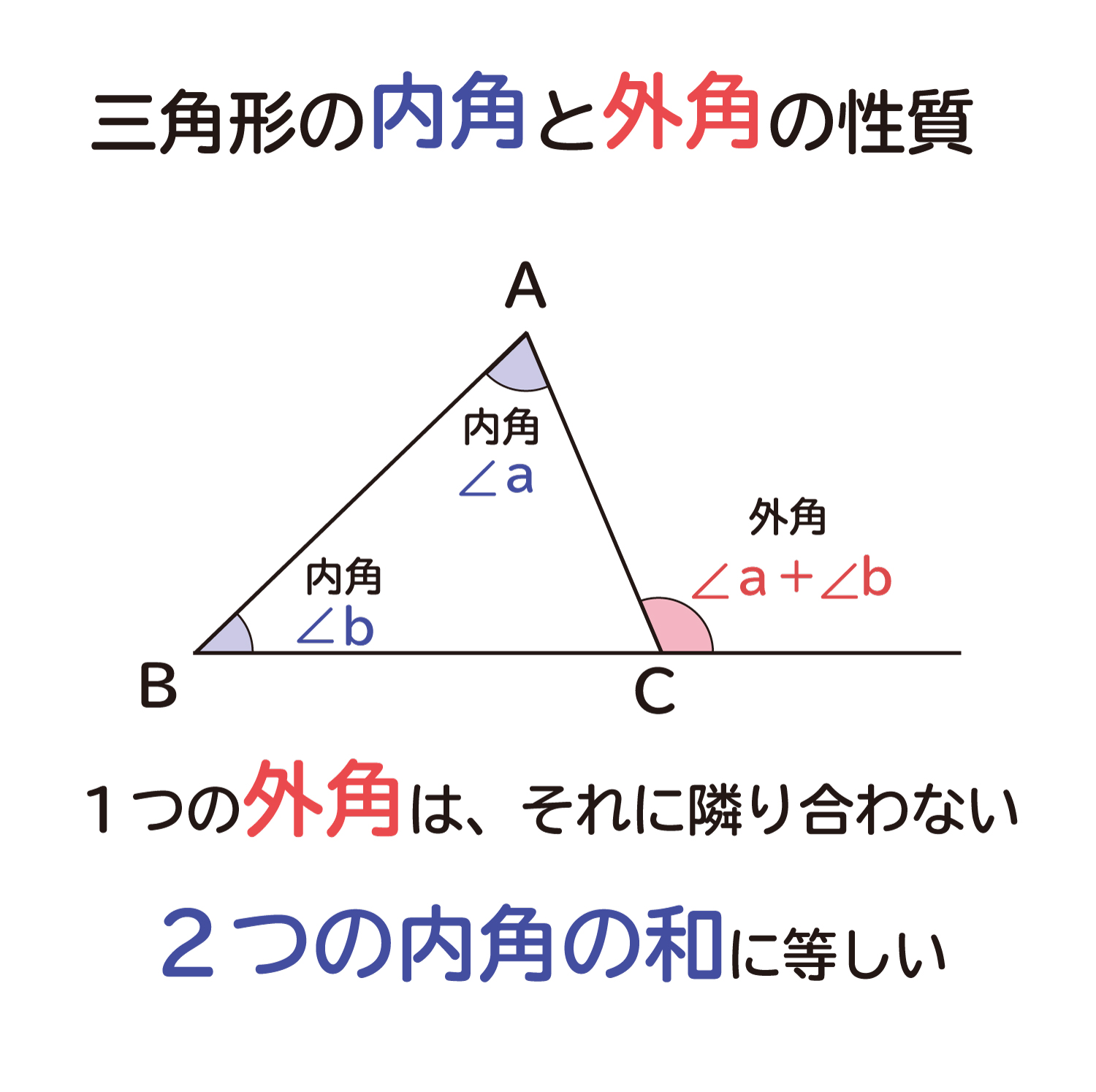



なぜ 三角形の1つの外角は それと隣り合わない2つの内角の和に等しい のか を説明します おかわりドリル
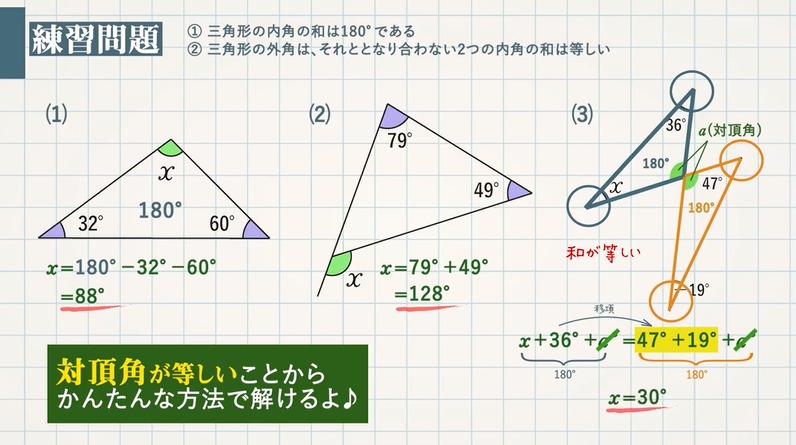



三角形の内角と外角の性質 教遊者
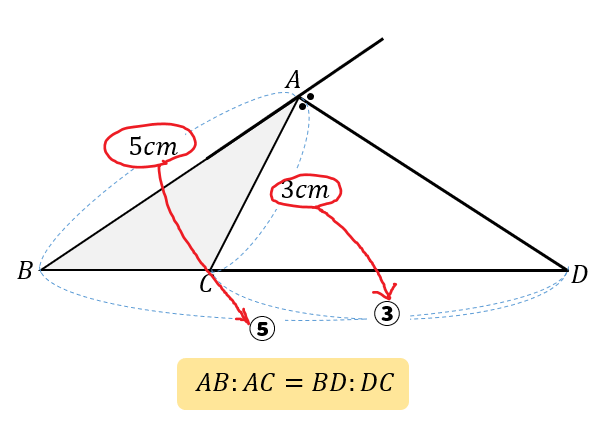



サクッと解説 角の二等分線と比の特徴となぜ について 数スタ
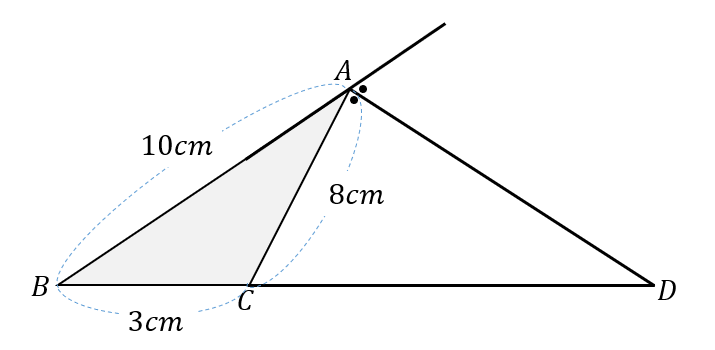



サクッと解説 角の二等分線と比の特徴となぜ について 数スタ
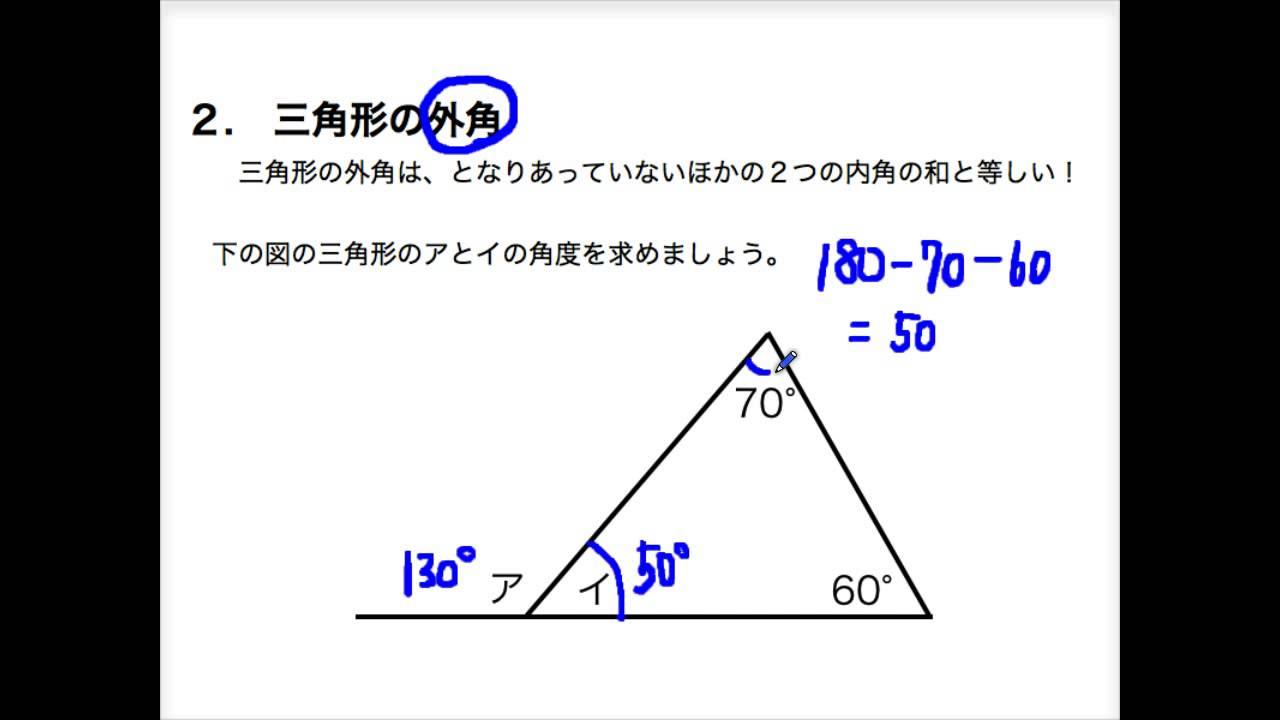



小学校5年 算数 三角形の外角 Youtube




七年級 三角形 內角和 外角 外角和定理
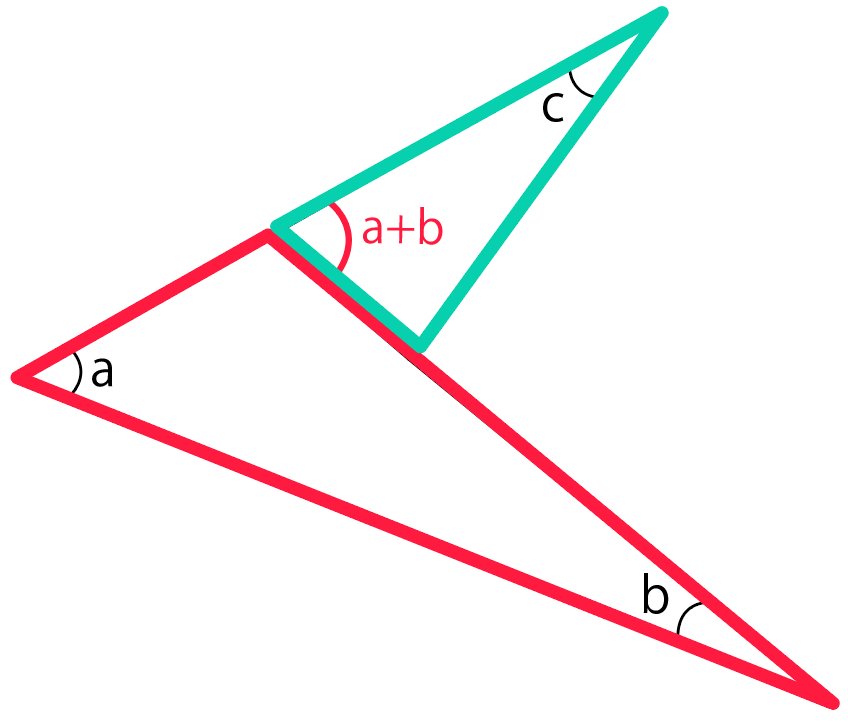



ブーメラン型四角形 凹四角形 の角度を求める方法 Qikeru 学びを楽しくわかりやすく
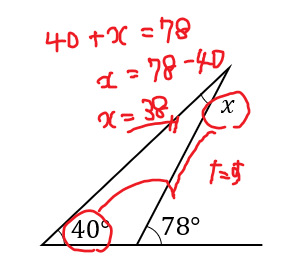



3分なるほど 三角形の内角 外角の性質について解説 数スタ
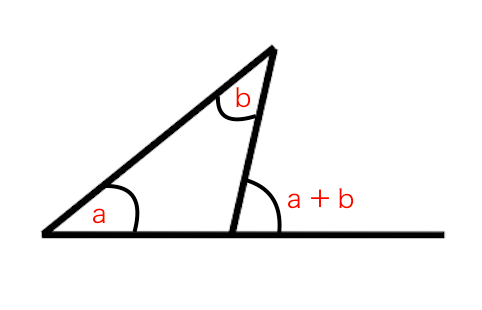



外角の定理とは 苦手な数学を簡単に
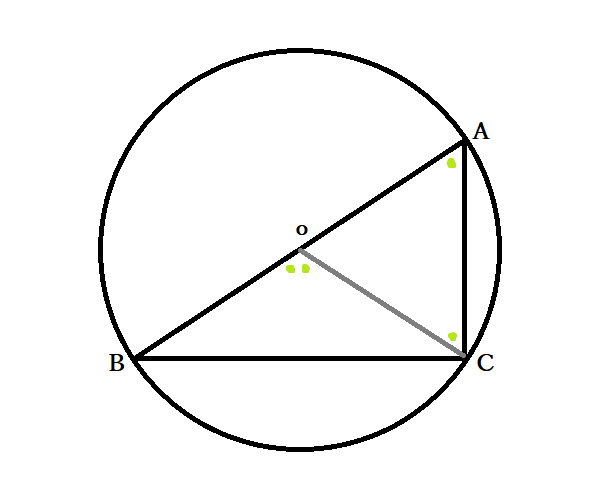



中3数学 円周角の定理とは 円周角と中心角の関係の証明法 円の性質の応用問題 中学 Curlpingの学びblog




三角形の内角の和は180度って証明できるの 三角形の外角の定理 公式 や問題アリ 遊ぶ数学




5分でわかる 余弦定理の公式と証明 使い方を簡単に理解しよう 高校生向け受験応援メディア 受験のミカタ




觀念 三角形內角和與外角和定理 數學 均一教育平台
コメント
コメントを投稿